Uppdaterad 19 januari 2026
Rak amortering & annuitet

I den här artikeln går vi igenom alla de ekonomiska och matematiska delarna i amortering och två olika typer av amortering. Dessa två typer kallas för rak amortering och annuitet och kräver viss förklaring för att du skall förstå dessa på bästa sätt.
När du ställs inför frågan om du skall välja mellan annuitet (annuitetslån) eller eller rak amortering så är det framförallt frågan kring hur du föredrar ditt amorteringstempo.
Mycket kortfattat förklarat så innebär rak amortering att du hela tiden betalar samma amortering vid varje tillfälle. Räntan kommer däremot att minska efter varje betalningstillfälle och därmed även din inbetalningstakt.
När du tar betalar av ditt annuitetslån betalar du istället samma summa varje år eller månad. Det här gör att räntedelen kommer att vara större i början av lånet och när denna minskar med tiden ökar istället amorteringsdelen. Summan du betalar varje månad är ändå densamma.
Med denna kortfattade förklaring går vi in på de mer matematiska delarna av dessa bägge begrepp och tar några räkneexempel.
Om räkneexemplet
I bägge exemplen räknar vi med en fast ränta för att det skall bli förståeligt. I verkligheten är det vanligt med en rörlig ränta varpå bägge exemplen haltar betänkligt. Den grundläggande informationen om vårt lån är:
- Lånebelopp: 60 000kr.
- Låneränta: 3% (0,03 i decimalform).
- Månadsränta: 3/12 = 0,25% (0,0025 i decimalform)
- Avbetalningstid: 2 år, dvs 24 mån.
Rak amortering
När vi här skall förklara både detta avbetalningssätt för lån så väljer vi först att amortera 2500 kr varje månad.
Med rak amortering menas att du vid varje inbetalningar betalar samma del amortering, i vårt fall 2500kr. Räntan varje månad beräknas på föregående månads resterande skuld och beräkningen för de två första månaderna blir i vårt exempel:
Första inbetalningen:
- Amortering: 2500kr
- Räntekostnad: 0,0025⋅60 000 = 150kr
- Inbetalning: 2500 + 150 = 2650kr.
- Resterande skuld: 57 500 kr.
Andra inbetalningen:
- Amortering: 2500kr
- Räntekostnad: 0,0025⋅57 500 = 143,75kr
- Inbetalning: 2500 + 143,75 = 2643,75kr.
- Resterande skuld: 55 000 kr.
Amorteringen kommer att vara konstant hela vägen genom avbetalningen medan alltså räntan sänks då den beräknas på restskulden. I nedanstående beräkning hittar du hela avbetalningsplanen för vårt exempel.
I det här räkneexemplet kan det också vara intressant att konstatera att den totala räntekostnaden blev 1875kr. Detta kan vi jämföra med den totala räntekostnaden då vi går in på annuitetslån.
Annuitet
Med annuitet menas istället att du varje månad (eller år om du väljer det) betalar exakt samma summa under perioden. Det här gör att räntedelen procentuellt sätt kommer att minska på beloppet medan amorteringsdelen ökar med tiden.
Det som är relativt svårt att få fram i den här typen av lån är den så kallade annuiteten. Det vill säga den summa som skall betalas varje månad för att täcka både ränteökningar och amorteringar under den period vi vill betala av lånet. Du som sysslat med aktier tidigare känner säkerligen igen metoden från det som kallas nuvärdesberäkning eller diskonteringsberäkning. Du som inte är så bevandrad kring dessa saker kommer antagligen tycka att det är en relativt krånglig formel.
Men själva formeln för att beräkna vilken annuitet som vi i vårt exempel får är
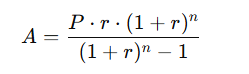
Där:
- A = Annuitetsbetalning per period
- P = Lånebeloppet (kapital)
- r = Periodränta (årlig ränta dividerat med antal betalningsperioder per år)
- n = Totalt antal betalningsperioder
Utifrån detta kan vi gå vidare och börja att modellera vår avbetalningsplan och vi gör som tidigare i den här artikeln att vi beskriver de två första inbetalningarna utifrån annuiteten 2579kr.
Första inbetalningen:
- Annuitet (Inbetalning): 2579kr
- Räntekostnad: 0,0025⋅60 000 = 150kr
- Amortering: 2579 – 150 = 2429kr.
- Restskuld kvar: 57 571 kr.
Andra inbetalningen:
- Annuitet (Inbetalning): 2579kr
- Räntekostnad: 0,0025⋅ 57 571 = 144kr
- Amortering: 2579 – 144 = 2435kr.
- Restskuld kvar: 55 136 kr.
När vi modellerar denna avbetalningsplan vidare så kommer den att se ut på följande vis:

När vi istället använder oss av annuitet kommer den totala räntekostnaden att bli 1893kr vilket är aningen högre än vid rak amortering.
Jämförelse av de bägge typerna av amortering
Det finns fördelar och nackdelar med bägge typerna av avbetalningsplaner så vilken modell just du väljer beror mycket på din egen situation och vad du tror passar just dig bäst. Det är också värt att återigen nämna att i bägge exemplen ovan så räknar vi på en fast (och ganska låg) ränta vilket inte alltid är fallet i verkligheten där räntan rör sig upp och ner.
Fördelar och nackdelar med rak amortering
Med den raka amortering hittar du fördelarna dels genom att den totala räntekostnaden kommer att bli lägre än vid motsvarande annuitetsbetalningar. Dina betalningar kommer även att minska med tiden vilket gör att lånekostnaden lättar med tiden.
Nackdelen är att du inte får samma jämna inbetalningstempo och att lånet kan vara lite tyngre i början av avbetalningstiden.
Fördelar och nackdelar med annuitet och annuitetslån
Vid annuitetslån är fördelen att du kommer att få ett jämnt avbetalningstempo. Du betalar samma summa varje månad eller år (förutsatt att räntan är fast) och det kommer även att gå snabbare och snabbare att betala av lånet då räntedelen minskar. Så har du en mer ansträngd ekonomi när du tar lånet kan detta skapa en lugnare och stabilare start.
Nackdelen är att den totala räntekostnaden blir högre med denna typ av amortering.
Amorteringskrav
För bolån finns ett amorteringskrav som infördes av Finansinspektionen. Enligt amorteringskravets regler måste man amortera en viss procentsats på sitt bolån varje år om man har en belåningsgrad och en skuldkvot som överstiger vissa nivåer.


Mycket bra och lättläst beskrivning av de olika begreppen som är lite krångliga att förstå vid första kontakten. Tack så mycket Mvh
Hejsan Daniel, bra att artikeln hjälpte dig att förstå dessa amorteringsbegrepp!
hej,
fin sida!
Jag fundera kring detta med att omvandla årsräntan till månadsränta. Varför dividerar du årsräntan med 12? I mina ögon borde du istället ta tolfte roten ur 1,03 eftersom ränta kommer in multiplikativit.
Hej, förstår hur du tänker men det är väl så att räntan i ett räkneexempel som detta inte kan anses förändras och framförallt inte bero på räntan månaden innan. Vi räknar med samma ränta varje månad här och därmed måste man dela årsräntan med 12 eller med 4 om man betalar kvartalsvis.
Hej, jag har bundit ett lån på t.ex 2 år med en ränta på 3,04 och amorterar med 1000 kr varje månad och får inbetalningskort varje månad med den räntan och amortering av 1000 kr, kan jag ändå dock amortera av lite mer om jag har möjlighet just den månaden för att få ner räntan ännu mer än beräknat följande månad?
Jag gör nämligen det med CSN lånet. Jag betalar alltid in mer än vad som står på inbetalningskorten och varje år går då lånet ner med mer än vad som är uträknat och räntekostnaden går då ner mer för varje år som jag får inbetalningskort i en snabbare takt. Kan jag göra det med bolån också?
Hej Lucie,
tack för din fråga. Generellt när det gäller bolån med bunden ränta så är det ofta avgiftsbelagt att amortera extra under perioden när räntan är bunden. Det för att banken gjort en beräkning av räntan under den bundna tidsperioden. Vill du amortera av bolånet så går det bra när du binder om dina lån. Du bör naturligtvis alltid undersöka med din bank vad som gäller vid extra amortering när räntan är bunden. Ett tips som du kan göra är att istället ha ett sparande under den bundna tidsperioden för att sen kunna amortera extra. Fråga din bank om extraamortering är försatt med avgift under den bundna tidsperioden. Hoppas att det här kan hjälpa dig, lycka till!
Med Vänlig Hälsning
Sofia
http://www.hittalanet.se
självklart har kunden möjlighet att skjuta in extra pengar för att få ner räntekostnaden s.k extraamortering!
Tokbra förklarat!
Du borde bli lärare.
Bra artikel, men hur blir skillnaden mellan rak amortering och annuitet om med samma månatliga belopp och inte har en fast löptid på lånet.
Antag att har ett bolån på 1.5 miljoner med rak amortering och betalar 10 000 kr i månaden i amortering plus ränta i dagsläget. Över tid som lånebeloppet sjunker kommer räntan att sjunka och mina månatliga utgifter minskar.
Om jag istället skulle ha ett annuitetslån och också betala 10 000 kr i månaden i amortering plus ränta tills hela lånet är avbetalt skulle väl lånet vara avbetalt fortare eftersom amorteringstakten ökar när räntan minskar?
Så i ett sådant här fall bör väl den totalt betalda räntan bli lägre med ett annuitetslån än ett lån med rak amortering?
Hej Niklas,tack för din fråga.Tyvärr är jag ingen matematiker, men vår kalkylator för lånekostnad beräknar den totala räntekostnaden. Där kan du också jämföra annuitet och rak amortering för att se skillnaden mellan dem.
Mvh
Sofia
Tack för svaret. Tyvärr kräver er lånekalkylator att man har en fast återbetalningstid istället för ett fast månadsbelopp så den kan inte användas för det fallet jag är intresserad av.
Hej Niklas,
Jag förstår inte riktigt vad du menar.
”Om jag istället skulle ha ett annuitetslån och också betala 10 000 kr i månaden i amortering plus ränta tills hela lånet är avbetalt skulle väl lånet vara avbetalt fortare eftersom amorteringstakten ökar när räntan minskar?”
I ett annuitetslån blir det samma summa varje månad men förhållandet mellan amortering och ränta ändras ju varje månad. Du betalar alltså olika mycket i både ränta och amortering vid varje inbetalning än vid föregående gång.
Med en enkel rimlighetsbedömning kan man komma fram till att du aldrig kan betala av lånet snabbare med annuitet på 10tkr/mån än rak amortering 10tkr + ränta, så länge räntan är > 0 %. För att betala snabbare måste du ju någon gång amortera MER än 10tkr i annuiteten för att någonsin komma ikapp den raka amorteringen, eftersom du med annuitet betalar mycket mer räntor i början av lånets återbetalningstid.
I Excel kan du för övrigt räkna ut hur många månader det skulle ta att beta av ett lån på 1,5 miljoner upplagd som annuitet med 10 tkr varje månad, för en viss ränta. Du kan sedan jämföra med antalet inbetalningar om du gör en rak amortering på 10 tkr varje månad. Rak amortering ger 150 inbetalningar (=12,5 år), och det antalet ändras ju inte oavsett vad räntan är. Annuitet med 10 tkr/månad ger 188 inbetalningar (=15,7 år) om räntan är 3 % under hela perioden. Med 1 % ränta blir det fortfarande 160 inbetalningar. Du kommer därmed ha betalat mycket mer i räntor totalt med annuitetslånet än med rak amortering.
Hej!
Det är redan någon som har frågat detta, men anser att svaret som gavs är felaktigt. När man delar årsräntan med 12 för att få månadsräntan så blir månadsräntan felaktig. Precis som frågeskrivaren skrev så är det korrekta sättet att räkna att ta 12 roten ur 1,03. För att på så sätt få fram förändringsfaktorn för månadsräntan. För att ta ett exempel:
Månadsräntan i detta fall blir ju 0,25%, alltså blir förändringsfaktorn 1,0025. Antag att du lånar 2 000 000, då kommer räntan för ett helt år att blir 2 000 000 x 1,0025^12 = 2 000 000 x 1,0304 (alltså en ränta som är 3,04 % och inte 3 %. Så räntan på ett helt år blir 60 831 istället för 60 000. Kanske inte en så väldigt stor skillnad, men trots allt ett felaktigt sätt att räkna ut.
Hej Christoffer! Tack för din kommentar, vi ska kika på detta!
Mvh
Sofia
http://www.hittalanet.se
Hej Christoffer,
Exemplet är korrekt. Du blandar ihop ränta för en hel period och för delar av den perioden. När man konverterar en periods ränta till delbelopp, t.ex. en årsränta till månadsränta, delar man helt enkelt periodens ränta lika för varje delperiod. I Excel görs detta genom att man får hålla koll på ifall den ränta man fyller i verkligen är för en period eller för många perioder. (Vanligast är att man tar årsräntan/12, eftersom man oftast räknar på månadsinbetalningar men utifrån en räntesats som gäller per år)
Med dina siffror: 3 % årsränta på ett lån på 2 000 000. Om du betalar in räntan varje månad och inte amorterar, så får du varje månad betala in 2 000 000 x 0,03 / 12 = 5000 kr. Gör detta 12 månader i följd och du har betalat in 12×5000 = 60 000 kr.
Alternativt kan du betala hela årsräntan efter ett år, och då betalar du 2 000 000 kr x 0,03 = 60 000 kr.
Däremot ska man använda exponent (’upphöjt till’) när du ska räkna ränta-på-ränta. Till exempel: sätt in 2 miljoner på ett konto med 3 % årsränta (eller 3 % på en period). Efter tolv år (perioder) har du 2 milj x 1,03^12 = 2,85 miljoner.
Dvs – om räntan är angiven som årsränta så räknar man också ut räntan på ett helt år och delar den över antal månader. Skulle räntan vara angiven per månad måste man däremot göra som du gör, och räkna ut ett års ränta genom att ta (månadsräntan+1)^12. Men det är mycket ovanligt att man i Sverige anger ränta för en månad i taget, utan man avser så gott som alltid just årsränta. (I USA är det vanligt med ränta per kvartal. Ser alltid lägre ut än årsränta, och det är avsikten också)
Hej,
Om jag skulle vilja amortera mer på ett annuitetslån, sjunker då min månadskostnad i och med detta? Eller kortas bara återbetalningstiden ner?
Hej! Jag undrar vad det beror på att man betalar mer försra dragningen av lånet? Är det någon sammamlagd ränta.
Hej!
Riktigt bra artikel som gör att man hänger med lite kring det här med annuitetslån.
Har ett exempel:
Ett lån på 30.000 kr, årsränta 5%, och betalning skall vara 1.000 kr / mån i 30 månader.
Blir det något specifikt att tänka på när det kommer till att räkna i månader istället för hela år?
Tack på förhand!
Hej,
Har just tagit ett billån i banken med räntan 3.48% och rak amortering.
Om jag på månadsräntan lägger på aviseringsavgift och uppläggningsavgift utslagen per månad och sen räknar ut hur många procent det blir, så får jag 4% medan bankens effektiva ränta uppges till 4.53%. (Jag delade årsräntan på 12 månader).
Beräknar banken räntan på återstående lånebelopp varje månad så sjunker ju räntebeloppet och effektiva räntan borde bli mindre.
Vad gör jag för fel? Får det inte att stämma.
Bilfirmans finansiär erbjöd annuitetslån på 7 års löptid och förhandlade ner räntan till 2.95% men effektiva räntan var ändå 4.5%.
Tyckte 7 år var lång tid. ”Dom flesta betalar av snabbare. Lånen blir aldrig så gamla” sade bilhandlaren. Om jag betalar av detta lån snabbare så har jag ju betalat relativt förmycket ränta i början eftersom räntebeloppet är större då. Jag uppskattar effektiva räntan till över 10%, kanske mer, om jag skulle betala av detta lån efter tex halva tiden, men jag klarar inte av att räkna ut det.
Valde i alla fall banklånet med 0.5% högre ränta för att få en lägre kreditkostnad. Banken erbjöd oxå automatiska avbetalningar utan aviseringsavgift.
Rätt eller fel…
Hej,
Som konstaterats blir totalkostnaden med ett annuitetslån nästan detsamma som för rak amortering om båda har samma löptid och räntan är konstant; annuitetslånet blir bara omkring 1 promille dyrare. På 100 000 kr alltså så lite som 100 kr. Mycket få skulle nog låta 100 kr skillnad över åtskilliga år fälla avgörandet mellan rak amortering och annuitet.
Istället finns det två huvudskäl till att just bilar oftast erbjuds med annuitetslån:
1) Annuitetslånet ger sken av att vara billigare, eller att man åtminstone får en lägre månadskostnad.
2. Ett avbrutet annuitetslån är mycket lönsamt för långivaren.
Annuitetslån för bilar erbjuds i princip alltid bara med mycket långa återbetalningstider, gärna 6-10 år. Men ytterst få köper en bil och verkligen behåller den i så lång tid, utan många vill byta redan efter 3-4 år. Vid rak amortering har man då betalat av mycket mer på lånet och har en lägre restskuld, än vid annuitet då man mest betalar räntor i början av lånets löptid. Den som erbjuder annuitetslånet tjänar alltså väldigt mycket mer på ett avbrutet annuitetslån än på ett lån med rak amortering. Ju tidigare in på lånet man vill avbryta, desto mer tjänar långivaren. Av den anledningen erbjuder man gärna 10 års återbetalningstid med ”låg” månadskostnad. I själva verket blir lånet dyrt när man vill byta bil redan efter 2-3 år. Just på bilar är detta extra dåligt ur ekonomisk synvinkel, då bilens värde minskar kraftigt i början av dess livscykel, och man borde därför göra amorteringar som åtminstone håller jämna steg med värdeminskningen. Det gör man inte med annuitetslån.